Learning With Mistakes

greyCTF finals 2024

Original LWE use field GF(prime). TFHE use Mod(2^n). I use GF(2^n) so that it’s still a field so obviously mine is gna be more secure lmao.
Author: JuliaPoo
10 solves

lwe.sage
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
from secrets import randbits
from Crypto.Util.number import bytes_to_long, long_to_bytes
import numpy as np
from hashlib import sha512

n = 500
qbits = 32
mbits = 4
q = 2**qbits
F = GF(q)
x = F.gen()

def int_to_F(n):
    return sum(b*x**i for i,b in enumerate(map(int, bin(n)[2:][::-1])))

def F_to_int(f):
    return f.integer_representation()

def gen_key():
    return np.array([b for b in map(int, format(randbits(n), "0500b"))], dtype=object)

def gen_a():
    return np.array([int_to_F(randbits(qbits)) for _ in range(n)], dtype=object)

def gen_noise():
    return int_to_F(randbits(qbits - mbits))

def encrypt_mbits(m, s):
    a = gen_a()
    f = np.vectorize(F_to_int)
    m = int_to_F(m << (qbits - mbits))
    return (f(a), F_to_int(np.dot(a, s) + m + gen_noise()))

def decrypt_mbits(c, s):
    a,b = c
    f = np.vectorize(int_to_F)
    a,b = f(a), int_to_F(b)
    return F_to_int(b - np.dot(a,s)) >> (qbits - mbits)

def encrypt_m(m, s):
    m = bytes_to_long(m)
    c = []
    while m != 0:
        mb = m & 0b1111
        c.append(encrypt_mbits(mb, s))
        m >>= 4
    return c[::-1]

def decrypt_m(c, s):
    m = 0
    for cb in c:
        m <<= 4
        mb = decrypt_mbits(cb, s)
        m += int(mb)
    return long_to_bytes(m)


# https://www.daniellowengrub.com/blog/2024/01/03/fully-homomorphic-encryption
message = b"Original LWE use field GF(prime). TFHE use Mod(2^n). I use GF(2^n)"
key = gen_key()
ciphertext = encrypt_m(message, key)
assert decrypt_m(ciphertext, key) == message

flag = b"grey{XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX}"
keyhash = sha512(long_to_bytes(int(''.join(map(str, key)), 2))).digest()
flag_xored = bytes([a^^b for a,b in zip(flag, keyhash)]).hex()

print(ciphertext)
print(flag_xored)
# sage lwe.sage > log

Quite a lot of code for my standards. The name implied I maybe had to understand LWE to try this, but I just went headfirst anyways and it went okay. Essentially, they give us the plaintext message (which happens to be the chall desc) as well as the ciphertext, and asks us to recover the key used in encryption.

I will just explain what each line in the core encrypt function does:

28

29

30
31

32



def encrypt_mbits(m, s):
    # `s` is the key, in this case an array of 500 randomly generated bits (0/1)
    a = gen_a()
    # `a` is an array of 500 randomly generated GF(2^32) polynomials
    f = np.vectorize(F_to_int)
    m = int_to_F(m << (qbits - mbits))
    # m (4-bit block of plaintext) is shifted to the left by 28 bits, then converted into a GF(2^32) polynomial
    return (f(a), F_to_int(np.dot(a, s) + m + gen_noise()))
    # np.dot(a, s) is dot product a⋅s, so add up the polynomials in `a` corresponding to 1s in `s`
    # add m
    # add noise, which is a randomly generated GF(2^28) polynomial

what is GF(2^n)

You may have heard of GF(p)\text{GF}(p), working under a prime field, where you can just take your operations (modp)\pmod{p}. GF(p)\text{GF}(p) is different though (NOT the same as Z/pnZ\mathbb{Z}/p^n\mathbb{Z}), you have to treat it more like a n-“bit” vector. For example, the number 99 (binary representation 1001) under GF(24)\text{GF}(2^4) can be treated as the 4-bit vector

(1001) \begin{pmatrix} 1\\0\\0\\1 \end{pmatrix}

The reason we use a vector is because each bit is now treated as being dealt with independently. Each row is added/subtracted (mod2)\pmod{2}, for example, 9+39+3 in GF(24)\text{GF}(2^4) would be

(1001)+(0011)=(1010)\begin{pmatrix} 1\\0\\0\\1 \end{pmatrix} + \begin{pmatrix} 0\\0\\1\\1 \end{pmatrix} = \begin{pmatrix} 1\\0\\1\\0 \end{pmatrix}

which is 10. You might notice that this basically corresponds with the xor operation if both were treated as integers (which is why CRC is basically dealing with GF(2n)\text{GF}(2^n)). As for the “polynomial” part, 9 being 1,0,0,1 in this case would be

1x3+0x2+0x+11x^3 + 0x^2 + 0x + 1

Which can help draw parallels with polynomial properties, but in this challenge it is not super necessary, so we can just treat it as bit vectors (I will keep calling it polynomial though). Back to the important line:

32
return (f(a), F_to_int(np.dot(a, s) + m + gen_noise()))

per encryption, we get a, the array of 500 random GF(228)\text{GF}(2^28) polynomials, as well as np.dot(a, s) + m + gen_noise().
Recall that s, the key, is an array of 500 randomly generated bits. For np.dot(a, s), we basically look at which indexes of s are 1, and add up the polynomials at those indexes in a. Then, we add our message as well as noise. But, the thing is that m is only 4 bits, and is shifted to the left by 28 bits before being added, so it lands in the first 4 bits of the 32 bit ciphertext. Conveniently, the noise from gen_noise can only be 28 bits, so you are basically adding:

lwe

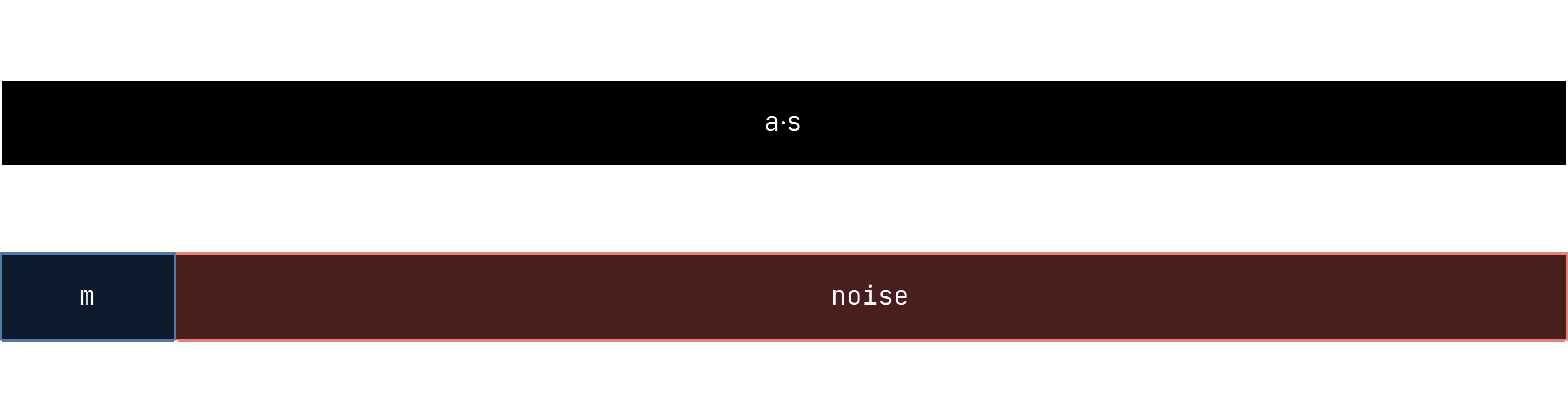
The thing is, since we are adding these two following the rules of a vector, m and the noise are basically completely independent, allowing us to focus on just the upper 4 bits of a⋅s that are added to m (and are not completely obliterated by noise).

whats the challenge

anyways, the message is actually encrypted as follows:

40
41
42
43
44
45
46
47
def encrypt_m(m, s):
    m = bytes_to_long(m)
    c = []
    while m != 0:
        mb = m & 0b1111
        c.append(encrypt_mbits(mb, s))
        m >>= 4
    return c[::-1]

AKA the message is split up into 33 4-bit components, and each is encrypted using the above. Since we have the original message and the ciphertext, we are given a, and have both m and (the upper 4 bits of) a⋅s + m (by subtracting, we now have a⋅s), and recall that we are trying to recover s with the key. Essentially, simplified, given a bunch of arrays of 500 4-bit integers each, find out the list of indexes, such that choosing those from each array and xoring them together produces the expected values of a⋅s for all 33 test cases we have. It is basically a knapsack-ish challenge, finding which elements to choose from each array that produces the desire output, except it has to be consistent across all 33 cases.

For some reason I am an LLL-addict so thats the first thing I tried (it would have worked, but I made a dumb mistake) but anyways this does not require that, its just a linear system. Think about one of the 4-bit blocks, where we have 500 4-bit integers, and we need to know which combination will add up to a⋅s:

(a[0]1a[0]2a[0]3a[0]4)s0+(a[1]1a[1]2a[1]3a[1]4)s1+⋯+(a[499]1a[499]2a[499]3a[499]4)s499=((a⋅s)1(a⋅s)2(a⋅s)3(a⋅s)4)\begin{pmatrix} a[0]_1\\a[0]_2\\a[0]_3\\a[0]_4 \end{pmatrix}s_0 + \begin{pmatrix} a[1]_1\\a[1]_2\\a[1]_3\\a[1]_4 \end{pmatrix}s_1 + \cdots + \begin{pmatrix} a[499]_1\\a[499]_2\\a[499]_3\\a[499]_4 \end{pmatrix}s_{499} = \begin{pmatrix} (a \cdot s)_1\\(a \cdot s)_2\\(a \cdot s)_3\\(a \cdot s)_4 \end{pmatrix}

Where we are solving for the values of s0,s1,⋯ ,s499s_0, s_1, \cdots, s_{499} that would satisfy this (but they have to be 0 or 1 only). But, remember that each row has to be done (mod2)\pmod{2} anyways, so if we work entirely under the field GF(2)\text{GF}(2), the values of ss would have to fall under 0 or 1 anyways! Of course, just this equation has many many solutions. But thats why we have 32 more cases to make the solution unique. These dont have to be separate equations, they can just be extended from this existing equations by making the aa vectors larger, since we are solving for the same ss values:

(a[0]1a[0]2⋮a[0]132)s0+(a[1]1a[1]2⋮a[1]132)s1+⋯+(a[499]1a[499]2⋮a[499]132)s499=((a⋅s)1(a⋅s)2⋮(a⋅s)132)\begin{pmatrix} a[0]_1\\a[0]_2\\\vdots\\a[0]_{132} \end{pmatrix}s_0 + \begin{pmatrix} a[1]_1\\a[1]_2\\\vdots\\a[1]_{132} \end{pmatrix}s_1 + \cdots + \begin{pmatrix} a[499]_1\\a[499]_2\\\vdots\\a[499]_{132} \end{pmatrix}s_{499} = \begin{pmatrix} (a \cdot s)_1\\(a \cdot s)_2\\\vdots\\(a \cdot s)_{132} \end{pmatrix}

This is an entirely linear system which can be solved easily (in my case, sage’s solve_right), so we have essentially won. Here’s my solve script:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# sage
import numpy as np
from numpy import array
from hashlib import sha512
from pwn import *
from Crypto.Util.number import bytes_to_long, long_to_bytes

read = open("dist-learning-with-mistakes/dist-learning-with-mistakes/log").read()
arr = eval(read[:-130])
enc = bytes.fromhex(read[-129:-1])

m = bytes_to_long(b"Original LWE use field GF(prime). TFHE use Mod(2^n). I use GF(2^n)")
c = []
while m != 0:
    mb = m & 0b1111
    c.append(mb)
    m>>=4
c=c[::-1]

NW = Matrix(GF(2),np.concatenate([[list(map(int, list(bin((j>>28))[2:].zfill(4)))) for j in arr[i][0]] for i in range(132)], axis=1)).T
W = vector(GF(2),list(np.concatenate([list(map(int, list(bin((arr[i][1]>>28)^^c[i])[2:].zfill(4)))) for i in range(132)], axis=0)))
key = list(NW.solve_right(W))

print(xor(enc,sha512(long_to_bytes(int(''.join(map(str, key)), 2))).digest()))

Flag: grey{I'm_flyin_soon_I'm-_rushing-this-challenge-rn-ajsdadsdasks}

lwe?

I did not even learn LWE to solve this, so I’m guessing why its vulnerable is because for LWE/TFHE as mentioned in the challenge description using GF(2)\text{GF}(2) or Z/2nZ\mathbb{Z}/2^n\mathbb{Z} means you cannot treat it as a vector, and noise is no longer easily separable from noise? oh well i’ll find out