HMAC-CRC

I came up with a new HMAC algorithm. How has no one thought of this before?
author: hadnot
15 solves

hmac-crc.py

from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
from binascii import crc32
import os

with open("flag.txt", "r") as f:
    flag = f.read().encode()

def CRC32(x):
    return int.to_bytes(crc32(x), 4, 'big')

key = os.urandom(16)
iv = os.urandom(8)
num_encryptions = 0

def encrypt(pt):
    global num_encryptions
    num_encryptions += 1
    if (num_encryptions > 200):
        # no more for you...
        return b""

    cipher = AES.new(key, mode=AES.MODE_CTR, nonce=iv)
    hmac = CRC32(key + pt + key)
    ct = cipher.encrypt(pad(pt + hmac, 16))
    return ct

def decrypt(ct):
    cipher = AES.new(key, mode=AES.MODE_CTR, nonce=iv)
    tmp = unpad(cipher.decrypt(ct), 16)
    pt, hmac_check = tmp[:-4], tmp[-4:]

    hmac = CRC32(key + pt + key)
    if (hmac_check == hmac):
        return pt

    return None

menu = """
Enter an option:
[1] Encrypt message
[2] Challenge
[3] Exit
> """

while True:
    option = input(menu).strip()
    
    if option == "1":

        message = input("Enter a message (in hex): ")
        try:
            message = bytes.fromhex(message)
            enc = encrypt(message)
            print(enc.hex())
            
        except Exception as e:
            print("Error!", e)
            exit(0)
        
        
    elif option == "2":

        for i in range(10):
            test = os.urandom(16)
            print(f"Encrypt {test.hex()}")

            enc = input("Answer (in hex): ")
            enc = bytes.fromhex(enc)
            
            if test != decrypt(enc):
                print("You failed!")
                exit(0)

        print(f"Wow! Here's the flag: {flag}")
            

    else:
        exit(0)

This is an oracle challenge, with a custom encryption. We can encrypt as many of our own messages as we want, but in the end we have to correctly encrypt 10 provided 16-byte messages to get the flag. Here is the encryption used:

def encrypt(pt):
    global num_encryptions
    num_encryptions += 1
    if (num_encryptions > 200):
        # no more for you...
        return b""

    cipher = AES.new(key, mode=AES.MODE_CTR, nonce=iv)
    hmac = CRC32(key + pt + key)
    ct = cipher.encrypt(pad(pt + hmac, 16))
    return ct

The key is 16 bytes, iv is 8 bytes (both securely random). We generate the HMAC as key + pt + key, then encrypt pt + HMAC with AES CTR. Where do we start?

Recap on what AES CTR is:

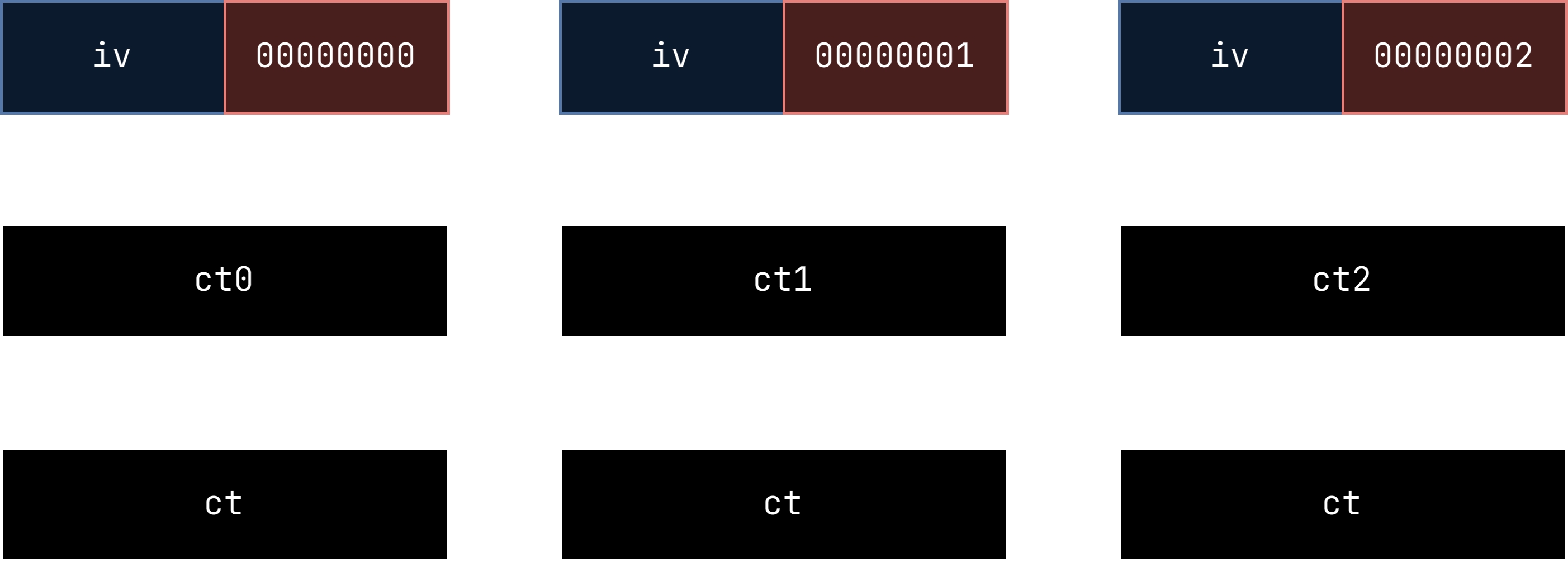
The part undergoing the actual cipher is just the iv + counter(counter is just incremented per block), then it is xored with the pt blocks. Hence, you might be able to guess when this is vulnerable. Since the only input of the plaintext is the xor, if we reuse the same iv, the block ct0 would appear again, and hence by xoring pt and then xoring any block m, we can forge an encryption of the block m.

Anddd they reuse iv. So that’s settled. We can forge the CTR encryption step if we know what we want to feed into it. But how? We are feeding pt + hmac. pt is fine, but what about hmac, being derived from CRC? Initially, I thought this was to do with the reversal of CRC, hence I tried to implement CRC32 including the specifications manually (bad idea; if you want to try; its not fun), but after that lead I realised something important about CRC.

What does CRC stand for? Cyclic redundancy check. Its a check, a checksum, by no means any encryption. So, it doesn’t need to defend against encryption. If you search it up, you may find out that CRC actually follows this very interesting xor property:

$$\text{CRC}(x \oplus y) = \text{CRC}(x) \oplus \text{CRC}(y) \oplus c$$

where $c$ depends on the lengths of $x$ and $y$. Usually this isn’t useful(in trying to abuse), since CRC isn’t something you would want to “forge”, after all its a checksum and anyone can calculate it. But here, where we don’t actually have the inputs into our AES-CTR which is pt + CRC(key + pt + key), but can do operations on it, it is useful.

The crux of the challenge is that once we start trying to encrypt the 10 server-given 16-byte messages to get the flag, we can’t go back and run the oracle, since we can’t predict what the pt‘s are. But, this CRC property implies that

CRC(key + pt + key) = CRC(key + \0 * 16 + key) ⊕ CRC(\0 * 8 + pt + \0 * 8) ⊕ c.

(c is a function of length, so its easy to calculate). And the first one doesn’t depend on pt so we can “precalculate” it, then when we are trying to get the flag, we can calculate the second one on the fly (since CRC can be calculated by anyone). I put quotes around “precalculate” because we can’t actually get its value, but because of the vulnerable way AES-CTR is used, we can still win:

AES(pt + CRC(key + \0 * 16 + key)) ⊕ \0 * 16 + CRC(\0 * 8 + pt + \0 * 8) ⊕ \0 * 16 + c
= AES(pt + CRC(key + \0 * 16 + key) ⊕ CRC(\0 * 8 + pt + \0 * 8) ⊕ c)
= AES(pt + CRC(key + pt + key)

Essentially, since AES and CRC are both “xor-forgeable”, and they are applied directly, we can use both tricks to encrypt any desired message on the fly. Here is the solve script I wrote on the day:

from pwn import *
from binascii import crc32
def CRC32(x):
    return int.to_bytes(crc32(x), 4, 'big')
conn = remote("challs.nusgreyhats.org", 32000r)
conn.recvuntil("> ")
conn.sendline("1")
conn.recvuntil(": ")
conn.sendline((b"\x00"*16).hex())
    res = bytes.fromhex(conn.recvline().decode().strip())
    print(res)

    conn.recvuntil("> ")
    conn.sendline("2")

    for _ in range(10):
        ct = bytes.fromhex(conn.recvuntil(": ").decode().split()[1])
        p1 = os.urandom(48)
        p2 = os.urandom(48)
        c = xor(CRC32(xor(p1,p2)), xor(CRC32(p1), CRC32(p2)))
        print(c)
        ans = xor(res[:16],ct) + xor(res[16:20], xor(CRC32(b"\x00"*16+ct+b"\x00"*16),c)) + res[20:]
        conn.sendline(ans.hex())
        
    print(conn.recv())

Flag: grey{everything_is_linear_algebra_a0945v832q}

Special thanks to this challenge for making me manually implement CRC32 for the first time.